FLOW STRUCTURE ON A ROTATING WING: EFFECT OF STEADY INCIDENT FLOW
Flow Structure on a Rotationg Wing: Effect of Steady Incident Flow: The flow structure along a rotating wing in steady incident flow is compared to the structure on a rotating wing in quiescent fluid, in order to clarify the effect of advance ratio J (ratio of free-stream velocity to tip velocity of wing). Stereoscopic particle image velocimetry leads to patterns of vorticity, velocity, and Q-criterion (constant values of the second invariant of the velocity gradient tensor), as well as streamlines, which allow identification of critical points of the flow. The effective angle of attack is held constant over the range of J, and the wing rotates from rest to a large angle that corresponds to attainment of the asymptotic state of the flow structure. Prior to the onset of motion, the wing is at high angle of attack and the steady incident flow yields a fully stalled state along the wing. After the onset of rotation, the stalled region quickly gives rise to a stable leading edge vortex. Throughout the rotation maneuver, the development of the flow structure in the leading edge region is relatively insensitive to the value of J. In the trailing-edge region, however, the structure of the shed vorticity layer is strongly dependent on the value of J. Further insight into the effects of J is provided by three-dimensional patterns of spanwise-oriented vorticity, spanwise velocity, and Q-criterion.
Principal Investigators: M. Bross and C. Ozen
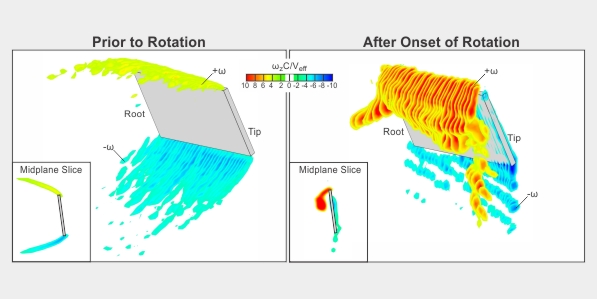
Stacked slices of spanwise vorticity shown represent a non-rotating wing in the presence of incident flow (left image); exhibiting a stalled state. The right image, taken shortly after the onset of rotation (at 36 degrees), has recovered from stall as indicated by the presence of a stable lift-generating flow structure called a leading-edge vortex.
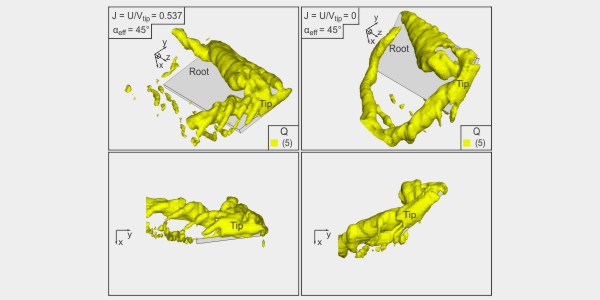
To further demonstrate the effect of J, three-dimensional representations of Q were constructed for hovering flight and forward flight. These representations show that a stable leading edge vortex along the span of the wing persists for extremes of advance ratio J. A large-scale loop vortex in the wake region, associated with the start-up process, exists at J = 0, but not at the largest value of J = 0.537. Moreover, the structure of the vortex in the root region of the wing, i.e., the root vortex, is fundamentally different for these extreme values of J.
